朴素贝叶斯算法的Python实现

发表于 2023年10月8日

介绍

朴素贝叶斯算法是一种常用的机器学习算法，用于进行分类任务。它的原理比较简单，就是基于贝叶斯定理和特征独立性假设来预测样本的类别。贝叶斯定理是一种用于计算条件概率的公式。它告诉我们如何在已知某个条件下，计算另一个条件的概率。在朴素贝叶斯算法中，我们将使用贝叶斯定理来计算给定某个特征的情况下，样本属于某个类别的概率。

朴素贝叶斯算法以概率原理为基础，在文本分类、情感分析和垃圾邮件检测等领域有其独特的应用。在本教程中，我们将展示朴素贝叶斯背后的数学概念，同时用Python实现该算法。

熵和朴素贝叶斯

在我们深入代码之前，我们先了解下朴素贝叶斯背后的数学原理。朴素贝叶斯的核心是利用条件概率，这个概念源自贝叶斯定理。这个定理使得算法能够根据先前的知识评估事件发生的概率，从而进行预测。

为了理解这个概念，我们引进熵的概念。在朴素贝叶斯的背景下，熵是作为衡量朴素贝叶斯算法质量好坏的一个标准，引导算法向着准确预测的方向前进。熵本质上是衡量数据集中的不确定性或随机性的指标。朴素贝叶斯算法的目标是最小化熵，从而最大化预测准确性。

贝叶斯定理

贝叶斯定理提供了一种计算假设概率的方法，基于我们的先验知识

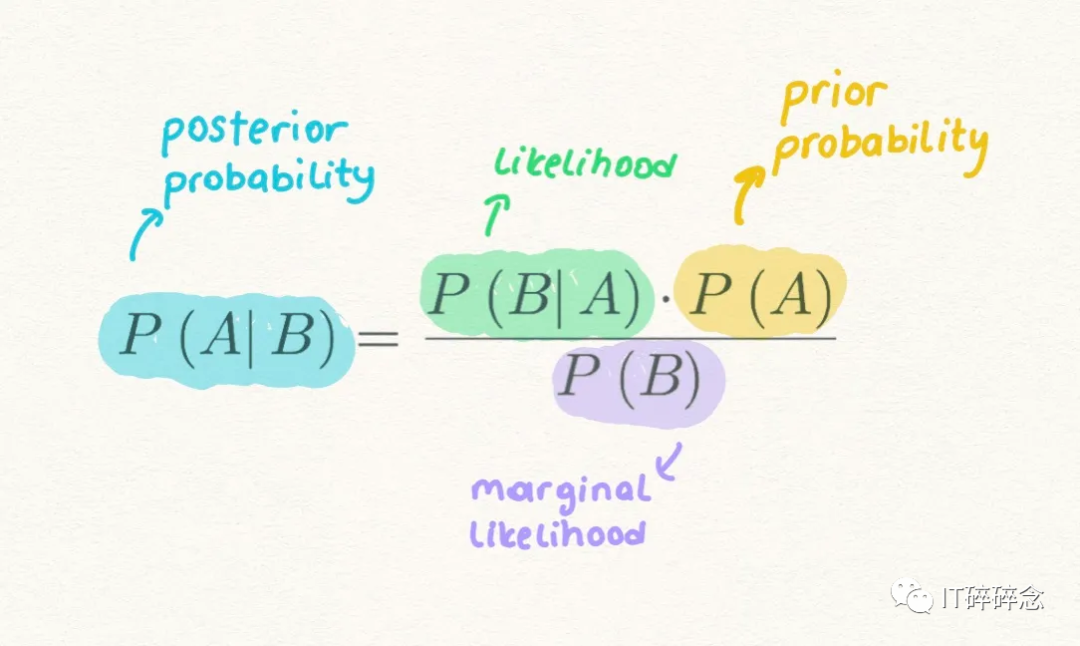
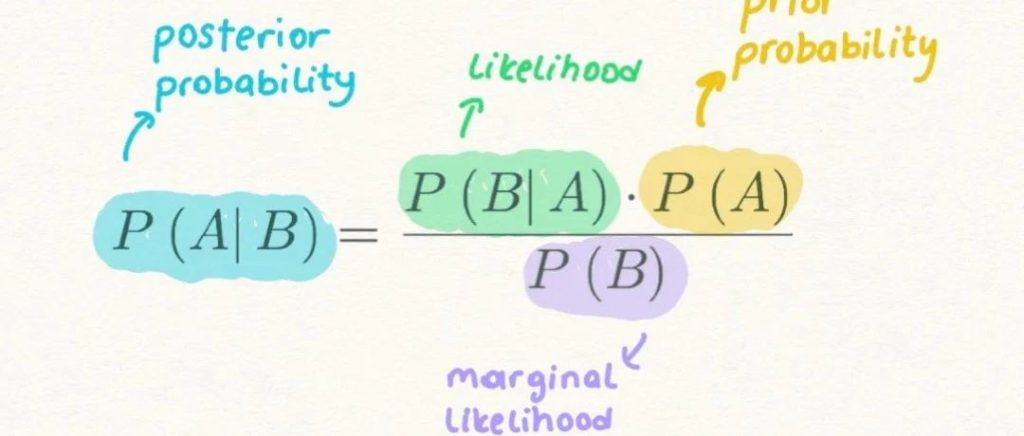
Prior Probabilityi先验概率：是在收集新数据之前事件发生的概率，即在看到任何新邮件之前，垃圾邮件的概率P（spam）。

Marginal Likelihood边际似然：是证据事件发生的概率，即P（money）是邮件中包含“money”的概率。

Likelihood可能性：是指在事件为真的情况下，证据发生的概率，即P(money|spam)是指在邮件为垃圾邮件的情况下，邮件中包含“钱”的概率。

Posterior Probability后验概率：是在证据信息被纳入考虑之后的结果概率，即P(spam|money)是指当邮件中包含“金钱”时，该邮件是垃圾邮件的概率。

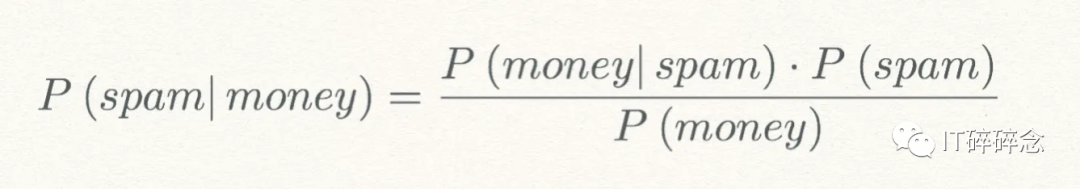
我们可以看到，我们正在从先验概率P(spam) 、P(money) 和 P(money|spam)中计算后验概率P(spam|money)。

最大后验概率（MAP）是具有最高后验概率的假设。在计算了多个假设的后验概率之后，我们选择具有最高概率的假设。

如果P(spam|money) > P(not spam|money)，那么我们可以说该邮件可以被归类为垃圾邮件。这是最大概率的假设。

朴素贝叶斯算法的Python实现

我们对朴素贝叶斯算法有一个概念基础，接下来我们开始使用Python来实现朴素贝叶斯算法。

在本教程中，我们将创建一个文本分类模型，用于区分垃圾邮件和合法邮件。

第一步，数据预处理

import pandas as pd
# 加载数据集data = pd.read_csv('spam_ham_dataset.csv')# 数据处理，转化成小写data['text'] = data['text'].str.replace('[^ws]', '').str.lower()

第二步，为了确保我们模型的有效性，我们需要将数据集分成训练集和测试集，这样我们能够更准确评估模型的效果。

from sklearn.model_selection import train_test_split
# 将数据集分成训练集和测试集train_data, test_data, train_labels, test_labels = train_test_split(data['text'], data['label'], test_size=0.2, random_state=42)

第三步，将训练数据中所有的单词放入一个Python集合对象。

# 创建一个vocabulary集合vocabulary = set()for text in train_data:    words = text.split()    vocabulary.update(words)

第四步，计算概率这里是朴素贝叶斯算法的关键之处——概率计算。我们将确定给定其相应类别（垃圾邮件或正常邮件）的单词的条件概率。

# 计算概率word_count = {}class_count = {'spam': 0, 'ham': 0}for word in vocabulary:    word_count[word] = {'spam': 1, 'ham': 1}for text, label in zip(train_data, train_labels):    words = text.split()    for word in words:        word_count[word][label] += 1        class_count[label] += 1

第五步，使用上面的概率计算结果，定义predict(text)预测函数

# 定义预测函数def predict(text):    words = text.split()    spam_prob = class_count['spam'] / (class_count['spam'] + class_count['ham'])    ham_prob = class_count['ham'] / (class_count['spam'] + class_count['ham'])    for word in words:        if word in vocabulary:            spam_prob *= word_count[word]['spam'] / class_count['spam']            ham_prob *= word_count[word]['ham'] / class_count['ham']    return 'spam' if spam_prob > ham_prob else 'ham'

第六步，评估模型，最后一步是使用测试数据集对模型的准确性进行评估。

# 评估模型correct = 0
for text, label in zip(test_data, test_labels):if predict(text) == label:correct += 1
accuracy = correct / len(test_data)print(f"Accuracy: {accuracy:.2f}")

结论

在这篇文章中，我们学会了朴素贝叶斯算法以其概率和通过熵的评价算法质量，再通过一个文本分类模型区分垃圾邮件和合法邮件，加深我们对朴素贝叶斯算法的理解。

Sprite

分类：

机器学习

标签：

机器学习

线性回归算法

一文讲解监督机器学习

评论已关闭。

Python编程

朴素贝叶斯算法的Python实现

Previous Post

Next Post