线性回归算法

发表于 2023年10月6日

在机器学习算法中，线性回归属于一个基础的算法。通常数据科学家和机器学习爱好者在学习过程的早期就会遇到这个算法。在本教程中，我们将逐步探索线性回归，从底层数学开始，深入研究梯度下降的理论，并最终在Python中进行实际实现。通过本教程的学习，你将对线性回归有扎实的理解，并能够将其应用于实际问题。

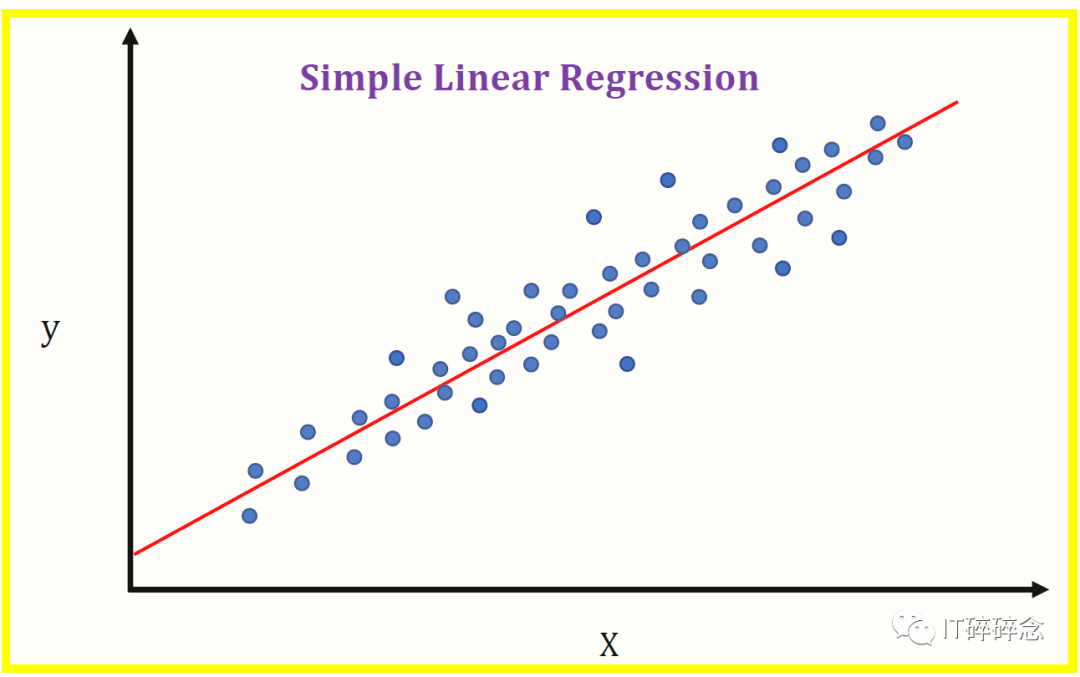
理解线性回归的数学原理

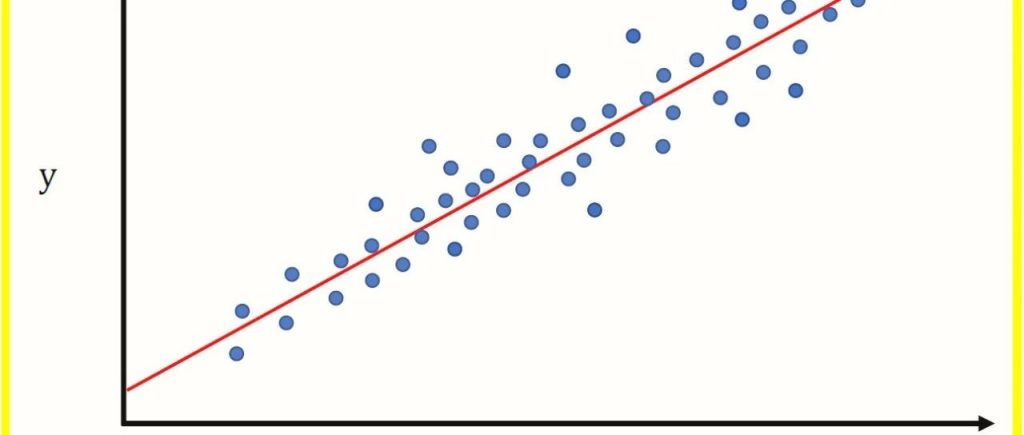
线性回归是在概率统计学中的一种统计方法，通过将线性方程拟合到观测数据点上，建模依赖变量与一个或多个独立变量之间的关系。其目标是找到最佳拟合线，使得预测值与实际值之间的差异最小化。

简单线性回归方程的数学表示为：y=mx+b

其中

y 是因变量
x 是自变量
m 是直线的斜率
b 是y轴截距

理解梯度下降

梯度下降是一种关键的优化技术，用于在线性回归中最小化预测值与实际值之间的误差。这个概念源于微积分，涉及迭代调整模型参数以达到最优值。

本质上，梯度下降法通过计算成本函数相对于模型参数的梯度，并沿着梯度的相反方向移动，以减小误差。该过程持续进行直到达到收敛，算法找到最小化成本的最优参数值。

在Python中实现线性回归

让我们深入探讨如何使用Python从头开始实现线性回归。我们将使用梯度下降法构建一个简单的线性回归模型。

import numpy as np
class LinearRegression:    def __init__(self, learning_rate=0.01, iterations=1000):        self.learning_rate = learning_rate        self.iterations = iterations        self.weights = None        self.bias = None    def fit(self, X, y):        num_samples, num_features = X.shape        self.weights = np.zeros(num_features)        self.bias = 0        for _ in range(self.iterations):            y_predicted = np.dot(X, self.weights) + self.bias            # 计算梯度            dw = (1/num_samples) * np.dot(X.T, (y_predicted - y))            db = (1/num_samples) * np.sum(y_predicted - y)            self.weights -= self.learning_rate * dw            self.bias -= self.learning_rate * db    def predict(self, X):        return np.dot(X, self.weights) + self.bias# 生成测试数据np.random.seed(42)X = 2 * np.random.rand(100, 1)y = 4 + 3 * X + np.random.rand(100, 1)# 实例化LinearRegression并拟和模型model = LinearRegression(learning_rate=0.1, iterations=1000)model.fit(X, y)# 进行预测X_new = np.array([[0], [2]])predictions = model.predict(X_new)print("Predictions:", predictions)

在这个实现中，我们定义了一个 LinearRegression 类，其中包含用于拟合模型（ fit ）和进行预测（ predict ）的方法。算法的核心在于 fit 方法，我们通过梯度下降迭代更新模型参数。

结论

在机器学习领域，线性回归作为一种基本算法，为我们后续理解更复杂的模型提供了基础。通过了解其数学基础并深入研究梯度下降的复杂性，我们成功地使用Python从零开始构建了一个线性回归模型。

在整个教程中，我们已经掌握了线性回归的本质，见证了它的数学表示，并利用梯度下降的力量进行优化。但线性回归只是进入机器学习世界的开始，后面我们会遇到更多算法，每个算法都有其独特的优势和应用。

Sprite

分类：

机器学习

标签：

机器学习

机器学习工程师都应该掌握的6个机器学习技能

朴素贝叶斯算法的Python实现

评论已关闭。

Python编程

线性回归算法

理解线性回归的数学原理

结论

Previous Post

Next Post