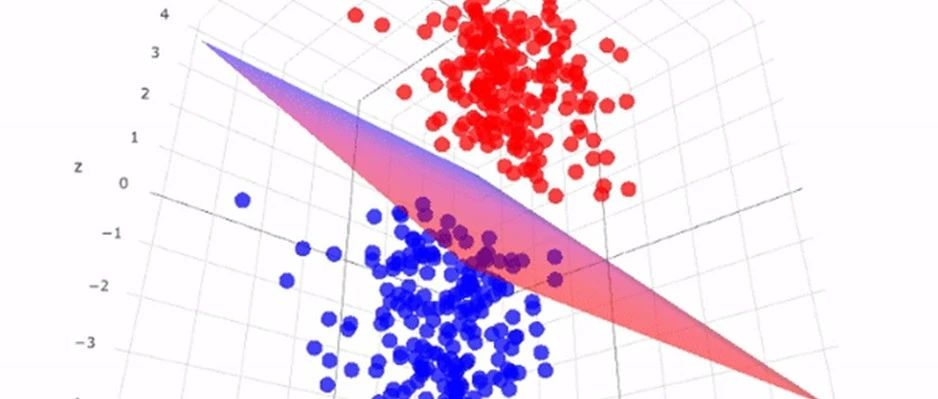
支持向量机（Support Vector Machine，简称SVM）是一种常见的机器学习算法，用于分类和回归分析。它的基本思想是找到一个最优的超平面，将不同类别的数据点分隔开来。

SVM 的核心概念是支持向量，即离超平面最近的数据点。这些支持向量决定了超平面的位置和方向。SVM 的目标是找到一个最大间隔的超平面，使得支持向量到超平面的距离最大化。这样可以使得分类结果更加准确和稳定。

除了线性可分的情况，SVM 还可以通过核函数将数据映射到高维空间，以处理非线性可分的情况。通过选取合适的核函数，SVM 可以更好地适应复杂的数据分布，并取得较好的分类效果。

SVM 在实际应用中具有广泛的用途。它在文本分类、图像识别、生物信息学等领域都取得了很好的效果。由于其理论基础扎实、算法稳定可靠，SVM 成为了机器学习中重要的工具之一。

关键术语

超平面

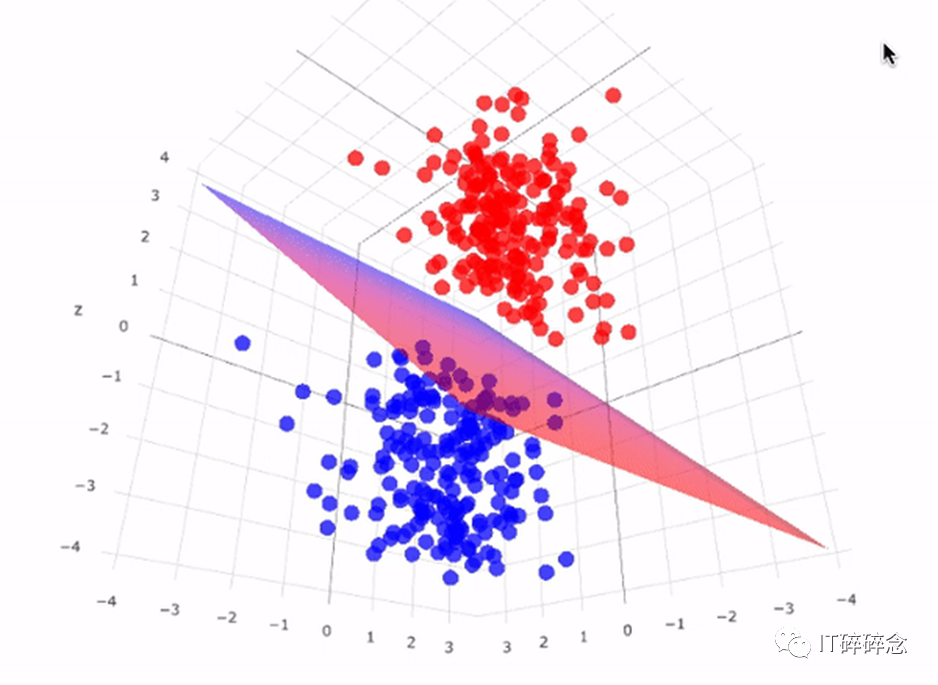
超平面是在高维空间中将数据点分隔到不同类别的决策边界。在二维空间中，超平面就是简单地将数据点分隔为两类的直线。在三维空间中，超平面是将数据点分隔为两类的平面。同样，在N维空间中，超平面具有（N-1）个维度。

通过评估数据点在超平面的哪一侧，可以对新数据点进行预测。超平面一侧的数据点被分类为属于一类，而超平面另一侧的数据点被分类为属于另一类。

间隔

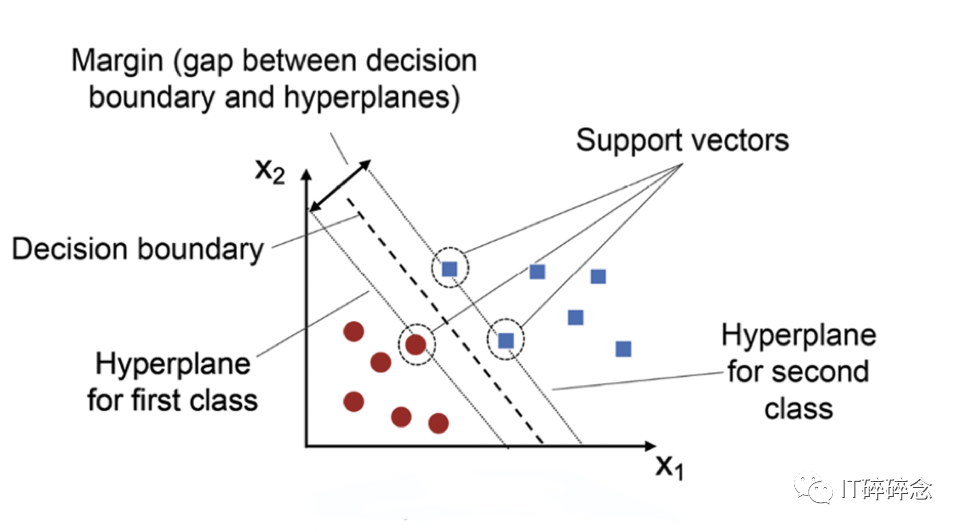
间隔是决策边界（超平面）与每个类别最近数据点之间的距离。SVM的目标是最大化这个间隔，同时最小化分类错误。较大的间隔表示对分类的置信度更高，因为它意味着决策边界与每个类别最近数据点之间有更大的间隔。间隔是特征空间中类别之间分离程度的度量。SVM旨在找到最大化该间隔的超平面，因此有时被称为最大间隔分类器。

支持向量

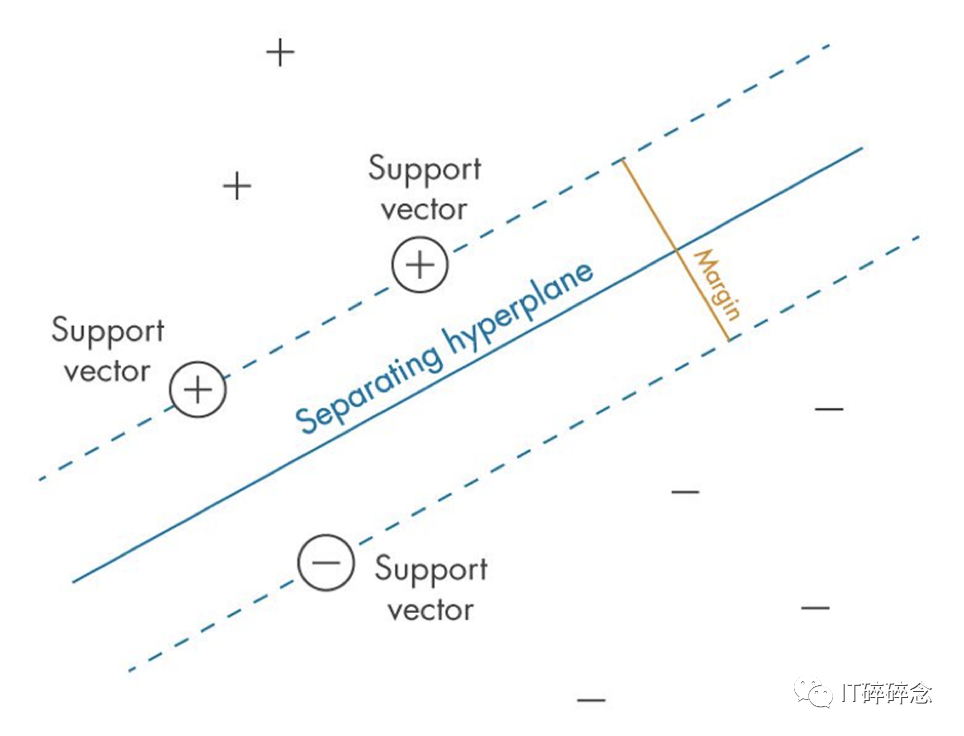
在支持向量机（SVM）中，支持向量是最靠近决策边界（超平面）的数据点。这些数据点很重要，因为它们决定了超平面的位置和方向，从而对SVM的分类准确性产生重要影响。实际上，SVM是以这些支持向量命名的，因为它们“支持”或定义了决策边界。支持向量用于计算间隔，即超平面与每个类别最近数据点之间的距离。SVM的目标是最大化这个间隔，同时最小化分类错误。

通过示例数据集理解SVM

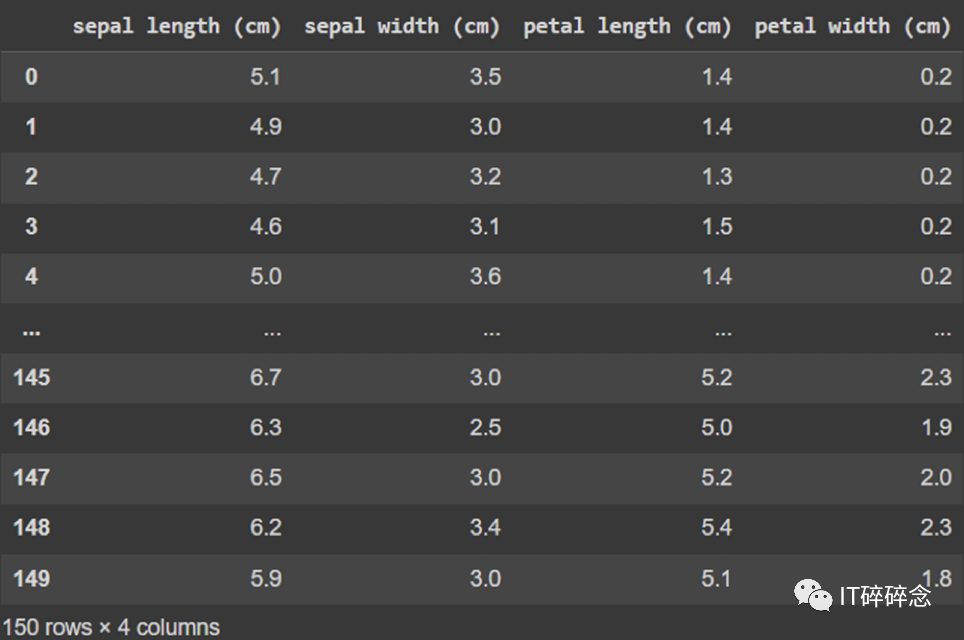来自Python的Scikit-learn库的鸢尾花数据集

我们有一个著名的数据集称为“鸢尾花”。该数据集有四个特征（列或自变量），但为了简化起见，我们只看其中两个特征：“花瓣长度”和“花瓣宽度”。然后将这些点绘制在二维平面上。

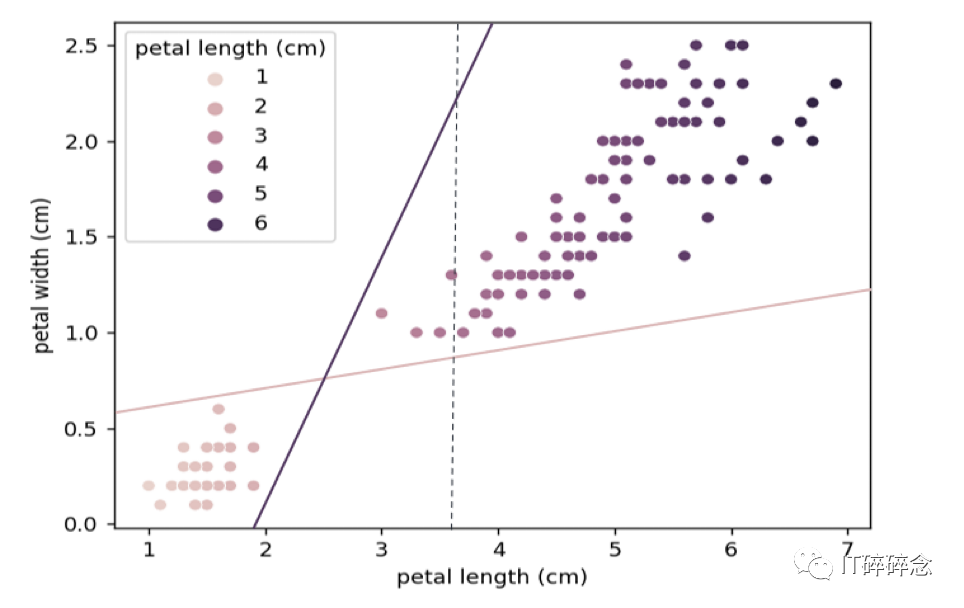
鸢尾花数据集由三条线（线性分类器）分隔，由深色、浅色和虚线表示。

较浅的点代表“山鸢尾”物种，较深的点代表“变色鸢尾”物种。

我们可以通过绘制线条，使用线性分类器来简单地对其进行分类。

深色和浅色线条准确地对测试数据集进行分类，但可能在新数据上失败，因为边界与各个类别的接近程度。而虚线分类器完全无用，并且对许多点进行了错误分类。

我们想要的是最佳的分类器。一个离整体类别最远的分类器，这就是SVM的用武之地。

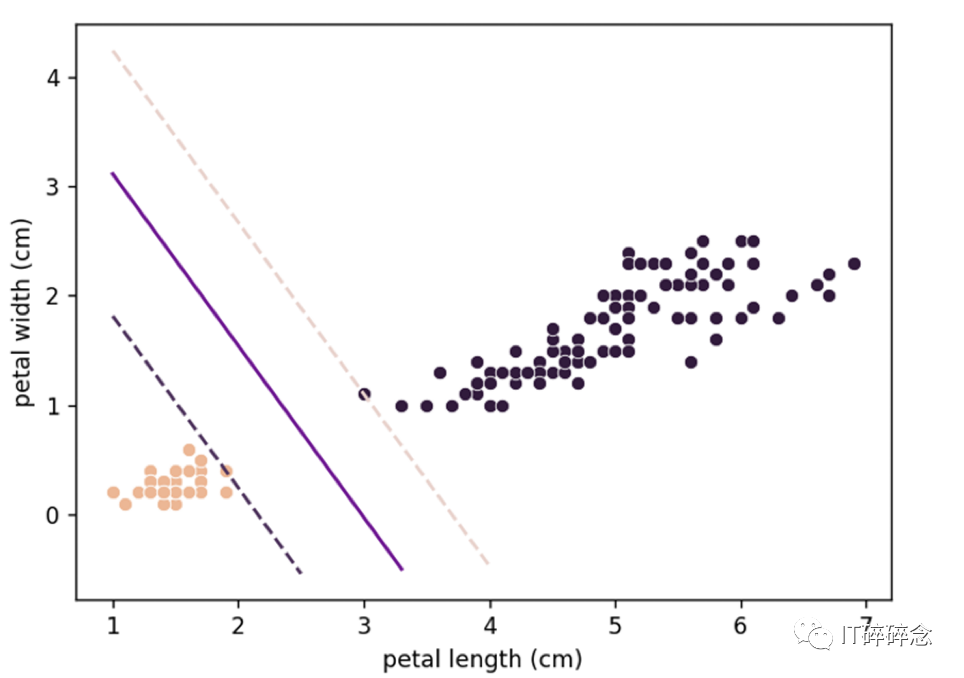
通过SVM模型获得的超平面将鸢尾花数据集分隔开，我们可以将SVM视为在类别之间拟合最宽可能路径（由平行虚线表示）。

这被称为“大间隔分类”。

注意：理论上，超平面正好位于支持向量之间。但在这里，它稍微靠近深色类别。为什么？这将在正则化部分中讨论。

通过类比理解（如果您已经理解，可以跳过这部分 🙂

我们可以将SVM视为一家建筑公司。二维平面是地图，两个类别是两个城市。数据点类比为建筑物。我们的目标是创建最佳的高速公路以最小化通过两个城市的交通，但我们受到可用区域的限制。

我们暂时将道路视为“直线”。（我们将在文章后面探讨非线性模型）

我们将合同交给了SVM建筑公司。SVM为了最小化交通量，希望最大化道路的宽度。它寻找两个城市之间最宽的土地区域。道路末端的建筑物被称为“支持向量”，因为它们限制或“支持”模型。高速公路被倾斜，以使两个城市都有足够的空间沿着它扩展。

这条将高速公路分隔的中心线代表决策边界（超平面），而边缘代表各个类别的超平面。高速公路的宽度就是间隔。

如果数据不是线性可分类的会发生什么？

当线性超平面不可行时，输入数据会被转换为一个更高维度的特征空间，在这个空间中可能更容易找到一个线性决策边界来分隔不同类别。

这是什么意思呢 ？

让我们看一个例子：

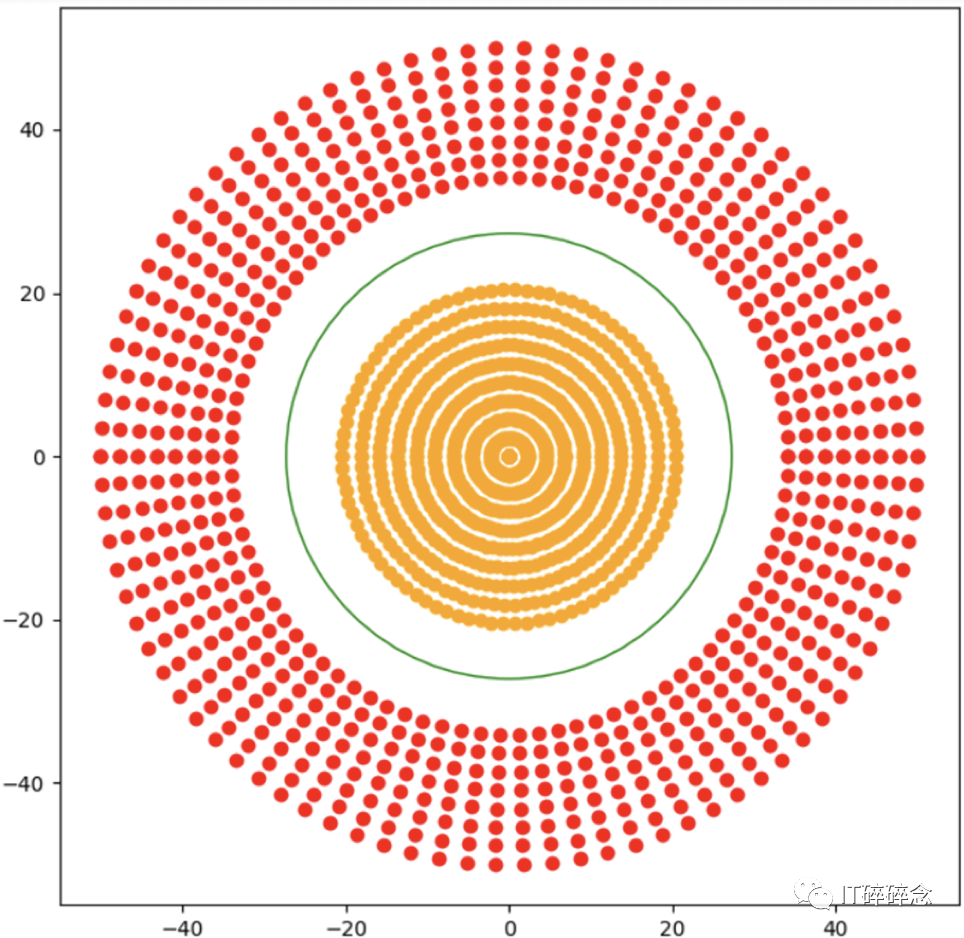
一个不可线性分离的数据集。

在上面的图中，不可能得到一个二维超平面，因此需要进行转换 (记得我之前说过如果高速公路不是笔直的情况)。

什么是转换或添加新特征？

我们有两个特征 X 和 Y，并且数据不可线性可分类。我们需要做的是在另一个维度上添加一个特征，这样如果数据被绘制出来，就可以线性可分。

维度中一个点的值就是该点的列值。为了添加另一个维度，我们必须创建另一列 (或特征)。

在这里，我们有两个特征 X 和 Y，需要一个第三个特征，它将是原始特征 X 和 Y 的一个函数，足以在线性三维空间中对数据进行分类。

我们取第三个特征 Z = f(x,y)；f 代表 X 和 Y 上的一个函数。这里只需要使用径向基函数(RBF)（测量欧氏距离）从原点开始。

Z = (X²+ Y²)^(1/2)

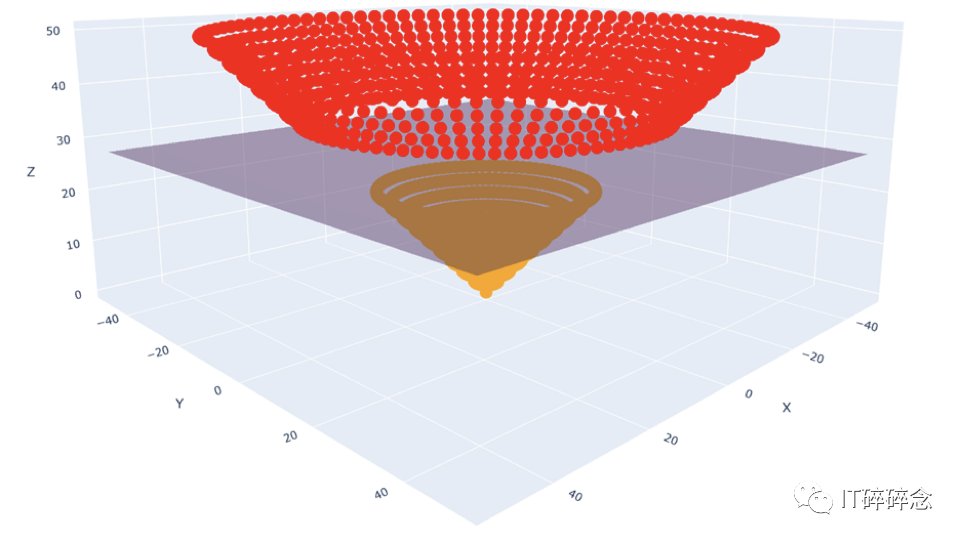
这些点在一个分割它们的三维超平面上绘制出来

这里的超平面很简单，只需在 X-Y 平面上创建一个与之平行的平面，并设置在特定高度。

这种方法存在的问题

这种方法的主要问题是计算量很大。

在这里，我们以同心圆的方式选择以原点为中心的点。假设这些点不是同心圆，但可以通过 RBF 分隔。那么我们需要每次将数据集中的每个点作为参考点，并计算相对于该点的所有其他点的距离。

因此，我们需要计算 n(n-1)/2* 个距离（n 个点中的 n-1 个点与每个点的距离，但一旦计算了 1-2 的距离，就不需要计算 2-1 的距离）。

时间复杂度

平方根的时间复杂度为 O(log(n))，而乘方和加法的时间复杂度为 O(1)。因此，要进行 n(n-1)/2* 次计算，我们需要 O(n²log(n)) 的时间复杂度。

但是，我们的目标是分隔类别而不是计算距离，因此我们可以省略平方根。(Z = X²+ Y²)

在这种情况下，我们将得到一个时间复杂度为 O(n²)。

但这还不是问题的关键，问题现在开始了

在这里，我们知道要使用哪个函数。但是只有二次多项式的度数限制下还有许多函数可供选择 (X, Y, XY, X² 和 Y²)。

我们可以使用这些 5 个特征以 ⁵C₃ 的方式得到 10 种组合方式。更不用说它们的线性组合的无限可能性了 (Z = 4X² + 7XY + 13Y², Z= 8XY +17X² 等等…)。

而且这仅适用于二次多项式。如果我们开始使用三次多项式，那么将会出现 X³, Y³, X²Y, XY²。

并不是所有这些都足够好以成为我们的附加特征。

例如，我以(X vs Y vs XY 作为特征) 开始：

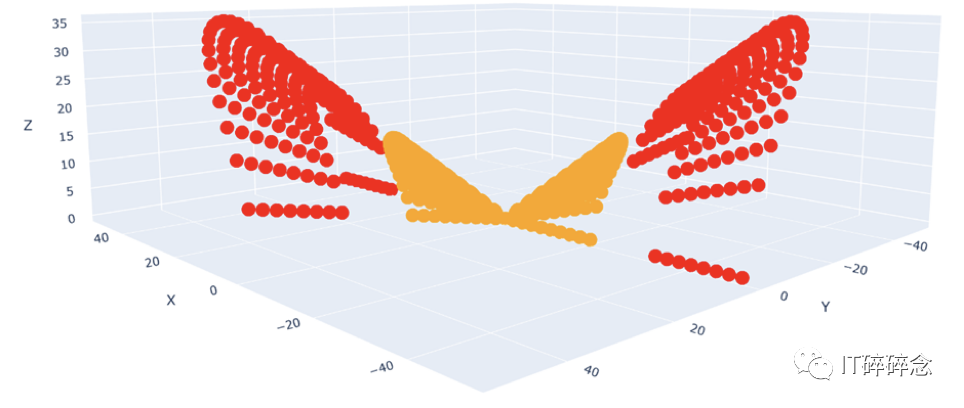
相同数据的 X vs Y vs XY 绘图，这个绘图不是线性可分类的 [这个图看起来像两只接吻的鸟的喙]。

所有这些绘图的计算都是徒劳的。

现在我们必须使用另一个函数作为特征，再次尝试。

比如，我使用(X² vs Y² vs XY 作为特征，是的，我替换了 X 和 Y)：

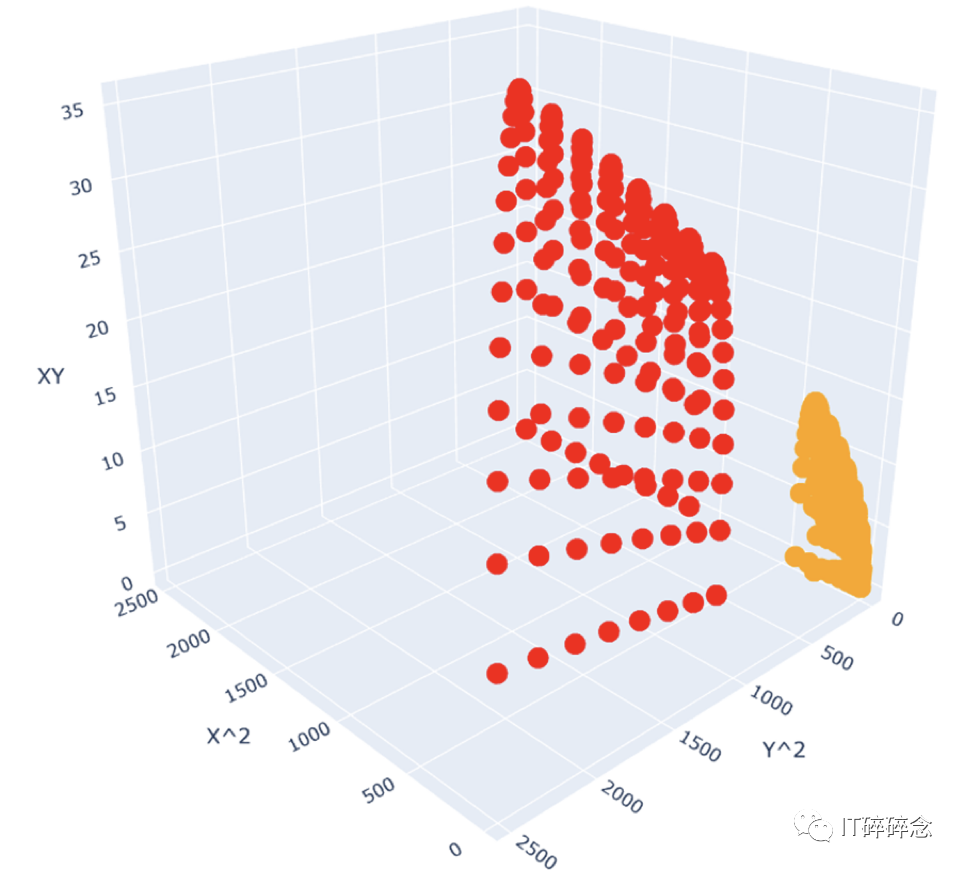
相同数据的 X² vs Y² vs XY 绘图，这个绘图是线性可分类的 [这个图看起来像一只鸟和它的喙]。

我看到了之前的数据，并注意到它不是线性可分的，因为黄色位于红色点之间。

由于两个黄色喙在中心相遇，并且其中一个喙向负 X 和负 Y 方向移动，所以我决定对 X 和 Y 进行平方，使得新的值从 0 开始，形成了仅在喙和鸟脸之间形成单一分离区域，而不是之前的两个。

这个绘图是线性可分的，通过这种方式，我们可以巧妙地重用 XY 的计算和绘图，以获得所需的特征来分隔数据。

但是，即使如此，这种方法也存在一些限制，比如只使用一个或两个特征数据集，以便在三维空间中获得绘图，而不是更多维度，还有我们大脑寻找模式以识别下一组特征的能力，如果第一个绘图没有模式，我们就必须再次猜测一个特征并从头开始。

即使我们在两步之内获得了所需的特征集，这种方法的速度仍然比我们实际使用的方法要慢。

我们使用的方法被称为核技巧。

内核技巧

内核技巧不是通过添加另一个维度/特征来找到点之间的相似性。

它不直接找到f(x,y)，而是计算这些点的图像的相似性。换句话说，我们不是找到f(x1,y1)和f(x2,y2)，而是取点(x1,y1)和(x2,y2)，并使用函数f(x,y)计算它们的输出有多相似；其中f可以是任意关于x,y的函数。

因此，我们不需要在这里找到一组合适的特征。我们以一种对所有特征集都有效的方式找到相似性。

我们使用高斯函数来计算相似性。

f(x) = ae^(-(x-b)²/2c²)

a：代表曲线峰值的高度

b：代表峰值中心的位置

c：是数据的标准差

对于RBF内核，我们使用：

K(X,X’) = e^-γ(|X-X’|²) = (1/ e^|X-X’|²) γ

γ：是表示模型线性性的超参数(γ ∝ 1/c²)

X，X’：表示两个点的位置向量

较小的γ（接近0）意味着更线性的模型，而较大的γ意味着更非线性的模型。

这里我们有两个模型（左边的γ=1，右边的γ=0.01），左边的模型更线性。

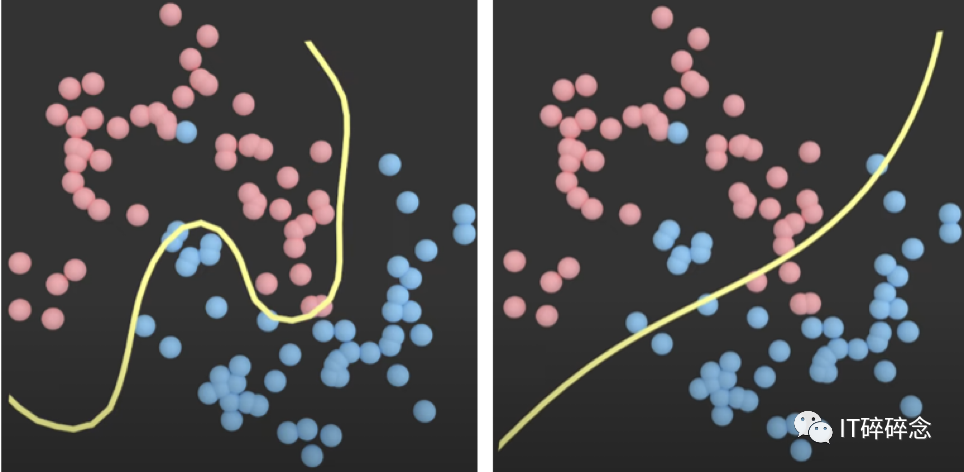
                                具有不同Gamma值的两个模型

那么为什么不让gamma的值非常高？低γ有什么用？

较大的gamma值可能导致过拟合，因此我们需要找到合适的gamma值。

下图显示了3个模型（从左到右γ=0.1，γ=10，γ=100）。左边的模型拟合得很准确，中间的模型过拟合，右边的模型过度拟合。

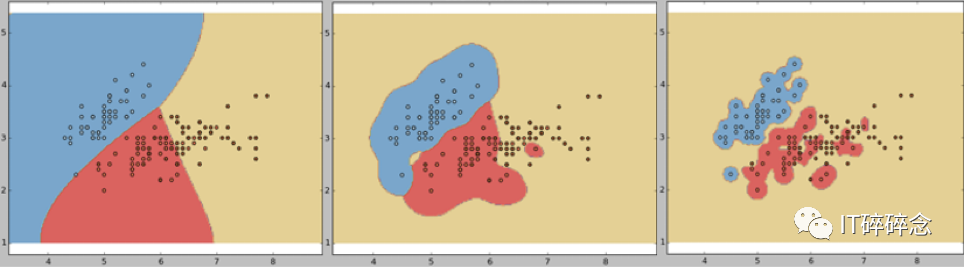
具有不同Gamma值的三个模型

时间复杂度

由于我们需要计算每个点与所有其他点的相似性，因此需要进行总共n*(n-1)/2次计算。

指数函数的时间复杂度为O(1)，因此总时间复杂度为O(n²)。

我们不需要绘制点，检查特征集合，进行组合等。这使得这种方法更加高效。

我们在这里使用不同的内核来优化计算。

我们有以下内核：

多项式内核

高斯内核

高斯RBF内核

拉普拉斯RBF内核

双曲正切内核

Sigmoid内核

第一类贝塞尔函数内核

ANOVA径向基函数内核

线性样条内核

无论我们使用哪个内核，都可以用比原始方法更少的计算得到结果。

为了进一步优化计算，我们使用“Gram矩阵”。

Gram矩阵是一个可以很容易存储和处理在内存中的矩阵，非常高效。

正则化和软间隔支持向量机

最后，进入一个新的主题 。

如果我们严格要求所有点都在正确的一侧，那么这被称为硬间隔分类（记得我展示的第一个SVM模型图）。

这种方法有两个问题。首先，它只适用于线性可分的数据，而不适用于非线性可分的数据（尽管大部分情况下可以线性分类）。

第二个问题是对异常值的敏感性。在下图中，红点作为左侧类别的异常值引入，它显著改变了决策边界，这可能导致在测试模型时对非异常值数据进行错误分类。

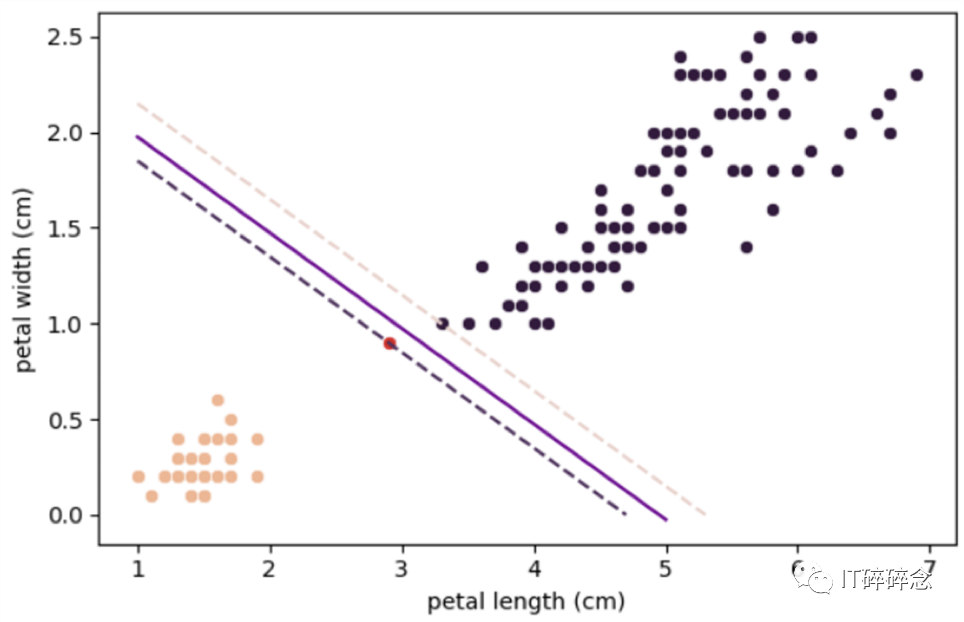
带有异常值的”Iris”数据集完全改变了决策超平面。

尽管该模型没有错误分类任何点，但它不是一个非常好的模型，并且在测试过程中误差会更高。

为了避免这种情况，我们使用软间隔分类。

软间隔是一种类型的间隔，它允许训练数据中存在一些错误分类的点。

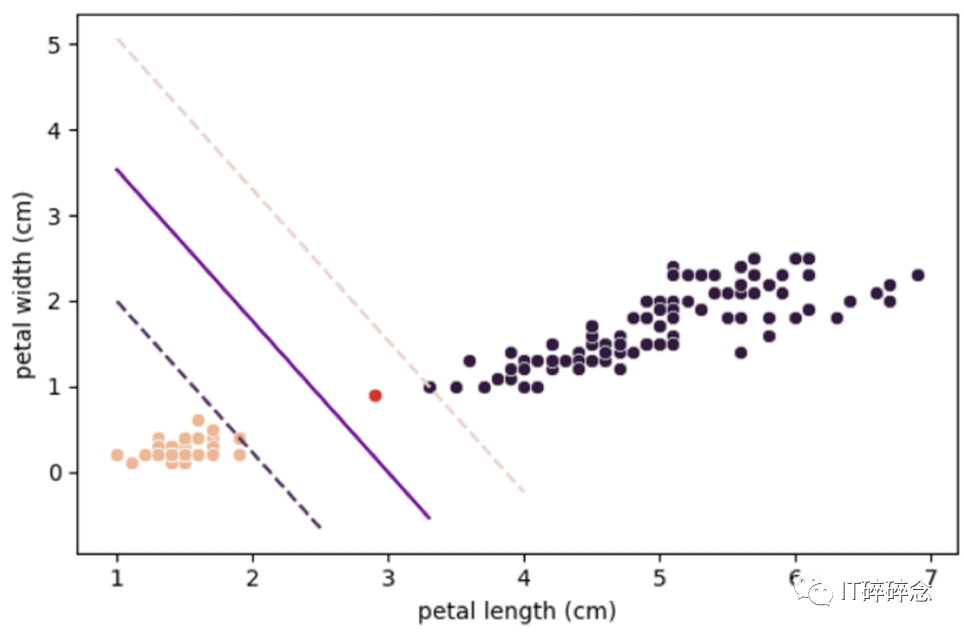
带有异常值的”Iris”数据集，但使用了软间隔分类。

在这里，软间隔允许一些错误分类的点位于决策边界的错误一侧。

即使训练数据集中存在错误分类，相对于先前的模型，整体性能在测试过程中会更好，因为它远离了两类数据。

但是我们可以通过删除异常值来解决异常值的问题，使用数据预处理和数据清洗，对吗？那为什么要使用软间隔？

它们主要用于当数据不是线性可分时，这意味着不可能找到一个完全分离类别的超平面而不产生任何错误，并且要避免异常值（硬间隔分类不可能）。例如：

“Iris”数据集（右侧类别是Iris Virginica，左侧类别是Iris Versicolor）不是线性可分的，但使用软间隔分类时，我们得到了一个最小错误分类的模型（相对于各类别超平面的0个次要错误分类）[5个主要错误分类，决策边界错误一侧]（C的值为100）。

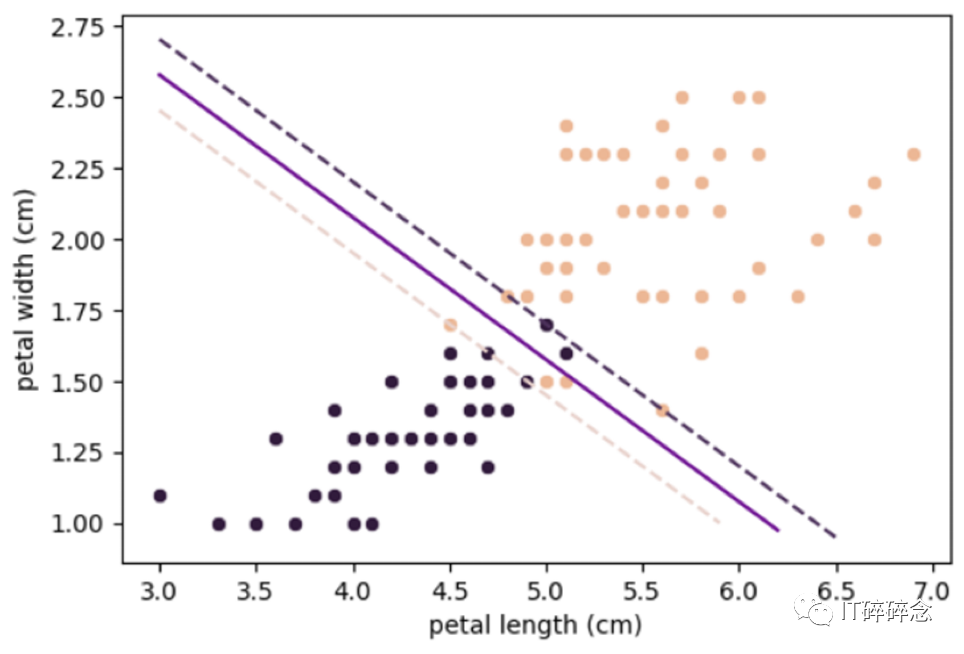
软间隔是如何工作的？

软间隔通过为每个数据点引入一个松弛变量来实现，这允许SVM容忍一定程度的误分类错误。容忍程度由一个称为正则化超参数C的参数控制，它决定了对最小化分类错误和最大化间隔应该给予多少权重。

它控制允许的误分类错误的容忍程度，C值越大，间隔越硬（对错误的容忍度较低），C值越小，间隔越软（对错误的容忍度较高）。

基本上，通过我们的类比，当无法在两个城市之间创建大型道路时，不是创建一个非常小的道路（针对异常值情况），而是通过移出一些人来创建一个更大的道路。

这对于移出的人来说可能不好（异常值被错误分类），但是整体高速公路（我们的模型）将更大（更准确）和更好。

在上面的情况中，如果无法创建道路，我们要求一些人离开并创建一条狭窄的道路。虽然较宽的道路对交通来说更好，但会导致大量的人出现问题（许多点被错误分类）。

正则化超参数’C’控制可以移出多少人（可以错误分类多少点或容忍度）来进行项目建设。

C值较高意味着模型的性质更加严格（对错误的容忍度较低）。而C值较低意味着模型的性质更加柔和（对错误的容忍度较高）。

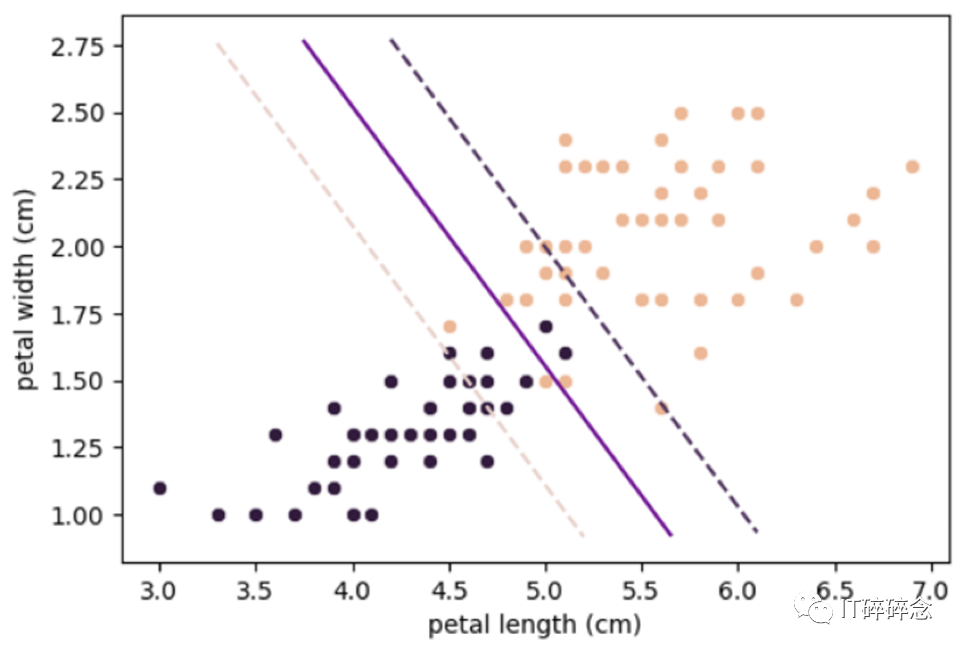
C值为1的相同模型（相对于类别的超平面存在12个次要错误分类）[4个主要错误分类，决策边界错误一侧]。

先前模型的较低C值（相对于100）容忍更多的错误分类，允许更多的人移出，因此建设了一条更宽的街道。

注意：较低的C值并不总是意味着更多的主要错误分类，有时可能意味着更多的次要分类。

在这种情况下，对于大多数一般情况来说，较低的C值往往会导致垃圾模型，会对多个点进行错误分类并降低准确性。

注意：低C值并不是简单地将原始路径扩大到达到所需的容忍水平。它意味着通过错误分类最大数量的点创建一个新的最宽路径，以使其低于容忍阈值。

C控制偏差/方差权衡。低偏差意味着模型对数据的假设很少或没有。高方差意味着模型会根据我们选择作为训练数据的内容而发生变化。

对于硬间隔分类，模型在更改数据时发生了显著变化（如果在超平面之间引入了新点），因此具有较高的方差，但它对数据没有任何假设，因此偏差较低。

软间隔分类模型几乎没有变化（由于对误分类数据的容忍），因此方差较低。但它假设我们可以误分类一些信息，并认为具有更宽余量的特定模型会产生更好的结果，因此偏差较高。

那么为什么使用低C值？为什么需要选择合适的值？

这类似于过拟合和欠拟合的现象，这种现象发生在C值非常高和C值非常低的情况下。

非常低的值会导致非常糟糕的结果，如上所示（类似于欠拟合的情况）。

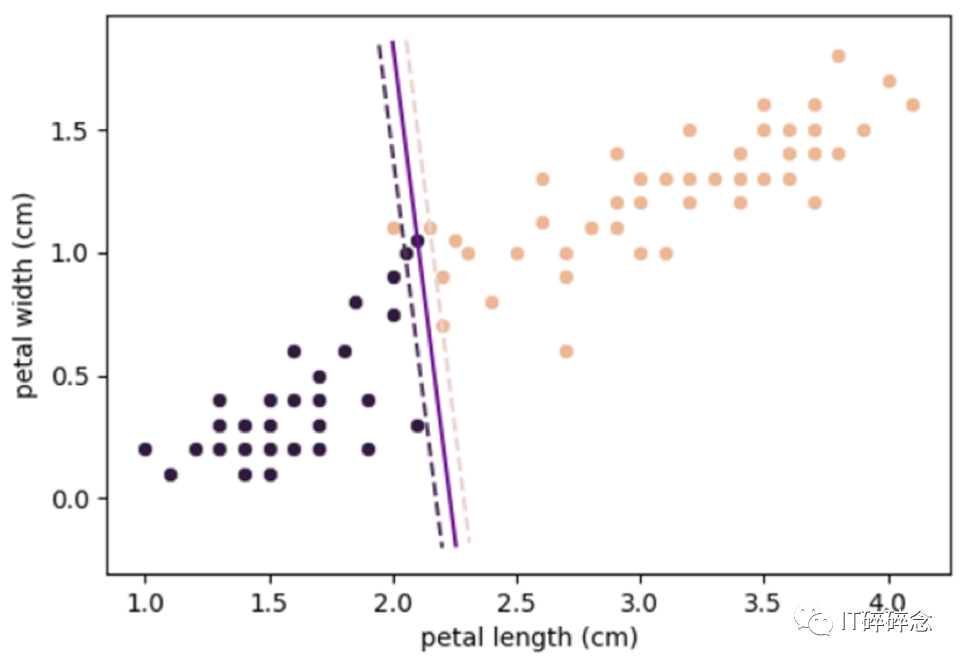
修改后的数据集显示了这种现象。

C = 1000的模型不合适，因为它在底部过于靠近左侧类别，在顶部过于靠近右侧类别，有可能错误地分类数据

使用支持向量机进行回归

支持向量机（SVM）通常用于分类，但也可以用于回归和分类。支持向量回归（SVR）是一种用于回归分析的机器学习算法。与传统的线性回归方法不同，SVR在连续空间中找到最适合数据点的超平面，而不是拟合数据点的直线。

与SVM相比，SVR试图最大化街道（间隔）中的点的数量，宽度由超参数ε（epsilon）控制。

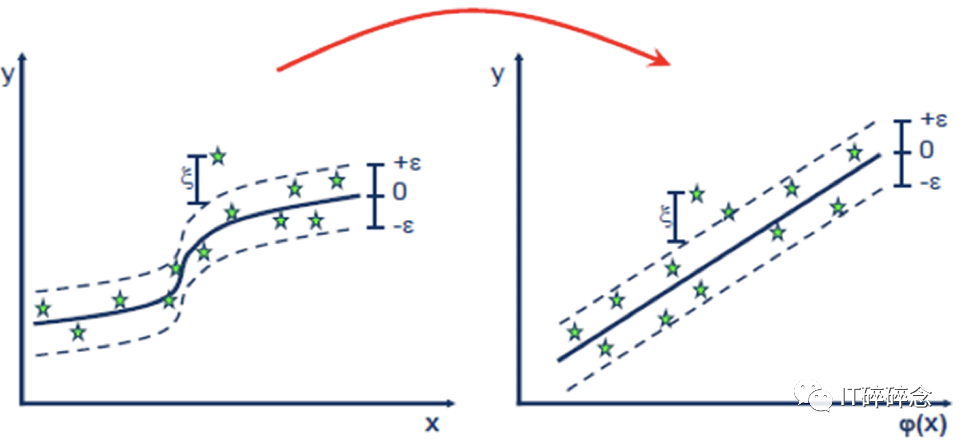
支持向量回归（SVR）使用决策超平面来预测值。

一个类比可以是在建筑物或房屋上方修建立交桥或桥梁，我们希望给尽可能多的房屋提供阴影，同时保持桥梁最细。

SVR希望将整个数据包含在其范围之内，同时试图最小化间隔，基本上是试图包围数据点。而线性回归希望通过使点到线的距离之和最小化来通过一条线。

SVR相对于普通回归的优点有：

1. 非线性： SVR可以捕捉输入特征与目标变量之间的非线性关系。它通过使用核技巧来实现这一点。相比之下，线性回归假设输入特征与目标变量之间存在线性关系，而非线性回归则需要大量计算。

2. 对异常值的鲁棒性： SVR相对于线性回归对异常值更鲁棒。SVR旨在将错误最小化到预测值周围的一定边界内，即ε不敏感区域。这种特性使得SVR不太受超出边界的异常值的影响，从而得到更稳定的预测结果。

3. 支持向量的稀疏性： SVR通常依赖于一部分训练实例，称为支持向量来构建回归模型。这些支持向量对模型有最重要的影响，代表了决策边界的关键数据点。这种稀疏性属性使得SVR在内存效率和计算速度上比线性回归更快，特别是对于大型数据集。此外，一个优点是在添加新的训练点后，如果它们位于边界上，模型不会改变。

4. 对模型复杂度的控制： SVR通过正则化参数C和核参数等超参数提供对模型复杂度的控制。通过调整这些参数，可以控制模型复杂度和泛化能力之间的权衡，这种灵活性是线性回归所不具备的。

SVM的应用和用途

支持向量机（SVM）已成功应用于不同领域的各种实际问题。以下是一些著名的SVM应用：

1. 图像分类： SVM广泛用于图像对象识别、手写数字识别和光学字符识别（OCR）。它们已被应用于过滤基于图像的垃圾邮件和用于安全、监视和生物识别的人脸检测系统。

2. 文本分类： SVM在文本分类任务中很有效，例如情感分析、垃圾邮件检测和主题分类。

3. 生物信息学： SVM已应用于生物信息学中的任务，例如蛋白质结构预测、基因表达分析和DNA分类。

4. 金融预测： SVM已用于金融应用中的任务，例如股市预测、信用评分和欺诈检测。

5. 医疗诊断： SVM已在医疗诊断和决策系统中使用。它们可以帮助诊断疾病、预测患者结果或识别医学图像中的异常模式。

SVM还应用于地球科学、市场营销、计算机视觉等其他领域，展示了它们在各种问题领域的多功能性和有效性。

总结

支持向量机（SVM）是一种强大的机器学习算法，用于分类和回归问题。它通过寻找最佳的决策边界来进行分类，并且具有一定的容错能力。SVM的核心思想是最大化间隔，即找到能够最好地分离不同类别的数据点的超平面。这使得SVM在处理复杂的数据集和具有高维特征的问题时表现出色。

SVM的一个重要特点是它可以使用不同的核函数来处理线性不可分的数据。通过使用核函数，SVM可以将数据映射到高维空间，从而使得线性不可分的数据在新的空间中变得线性可分。这种能力使得SVM在处理非线性问题时非常有用，例如图像分类、文本分类和生物信息学等领域。

除了分类问题，SVM还可以用于回归问题。支持向量回归（SVR）是一种使用SVM进行回归分析的方法。与传统的线性回归方法相比，SVR通过找到最适合数据点的超平面来进行回归，而不是拟合数据点的直线。这使得SVR能够应对非线性的回归问题，并具有对异常值的鲁棒性。

SVM在多个领域都有广泛的应用。在图像分类中，SVM被广泛应用于对象识别、手写数字识别和光学字符识别（OCR）等任务。在文本分类中，SVM在情感分析、垃圾邮件检测和主题分类等方面表现出色。在生物信息学中，SVM被用于蛋白质结构预测、基因表达分析和DNA分类等任务。此外，SVM还在金融预测、医疗诊断、地球科学和市场营销等领域展示了其多功能性和有效性。

总之，支持向量机是一种强大的机器学习算法，适用于分类和回归问题。它具有处理线性不可分数据和非线性问题的能力，并在多个领域展示了出色的应用性能。